Взвешивание
Вес термина в документе состоит из трех различных типов взвешивания термина: локального, глобального и нормализации. Вес термина описывается в уравнении 2.
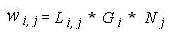Уравнение 2.
где Li, j - локальный вес термина i в документе j, Gi- глобальный вес термина i, а Nj - фактор нормализации для документа j. Локальные веса - это функции того, как часто каждый термин встречается в документе, глобальные веса - это функции того, как часто документы, содержащие каждый термин, встречаются в подборке документов, а фактор нормализации корректирует несоответствия, возникающие из-за разной длины документов.
В классической модели Пространственного Вектора Термина
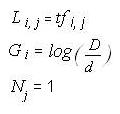Уравнения 3, 4 и 5
что сводится к хорошо известной схеме взвешивания if*IDF, описанной в уравнении 6
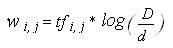Уравнение 6.
где log(D/di) - инверсная частота документа (Inverse Document Frequency - IDF), D - количество документов в подборке (размер базы данных), а di - количество документов, содержащих термин i.
Уравнение 6 - только один из многих вариантов взвешивания терминов, которые можно найти в литературе, посвященной векторам терминов. В зависимости от того, как определены L, N и G , для документов и запросов могут быть предложены различные схемы взвешивания.
Значения KD как оценка веса терминов?
Значения KD могут быть соотнесены с весом терминов только так, как описано в уравнении 7:
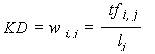Уравнение 7.
это при условии, что глобальный вес игнорируется, а фактор нормализации переопределяется в зависимости от длины документов, описанной в уравнении 8
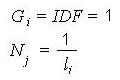Уравнение 8.
Однако, Gi = IDF = 1 ограничивает размер подборки D десятикратным количеством документов, содержащих термин (D = 10 * d), а Nj = 1 / lj не предусматривает фильтрацию стоп-слов. Эти условия не учитываются в коммерческих поисковых системах.
Использование вероятностной схемы вектора термина, в которой IDF определяется согласно уравнению 9,
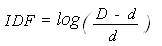Уравнение 9.
тоже не помогает, так как условие Gi = IDF = 1 подразумевает, что D = 11 * d. Дополнительные неосуществимые ограничения можно вывести для других схем взвешивания, когда Gi = 1.
Подытоживая вышесказанное, хочется отметить следующее. Предположение, что значения KD можно использовать для оценки веса терминов, или что эти значения можно использовать в целях оптимизации, приводит нас к определению "плотности ключевого слова нонсенс".
Список документов:
The Fractal Geometry of Nature, Benoit B. Mandelbrot, Chapter 38, W. H. Freeman, 1983.
From Complexity to Creativity: Computational Models of Evolutionary, Autopoietic and Cognitive Dynamics , Ben Goertzel, Plenum Press (1997).
Fractals and Sentence Production, Ben Goertzel, Ref 2, Chapter 9, Plenum Press (1997).
The Algorithmic Beauty of Plants, P. Prusinkiewicz and A. Lindenmayer, Springer-Verlag, New York, 1990.
Topic Analysis Using a Finite Mixture Model, Hang Li and Kenji Yamanish.
Improving the Effectiveness of Information Retrieval with Local Context Analysis, Jinxi Xu, W. Bruce Croft.
